Leetcode No.62 Unique Paths
2022/11/12The solution to the leetcode no.62 Unique Paths. Medium level.
algorithm
dynamic programming
dfs
Question
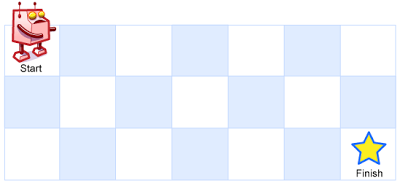
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
输入:m = 3, n = 2
输出:3
-> m
[0][ ][ ]
[ ][ ][x]
Solution
a. DFS
My first thought was DFS to solve this problem.
- Every step has two directions:
xory. - To reach the destination, the robot's
xshould be less thanmandyshould be less thann. - When
xis equal tomandyis equal ton, the robot reaches the destination.
Here is the code:
python
def uniquePaths(m: int, n: int) -> int:
x, y = 1, 1
ans = [0]
def dfs(x, y, m, n):
if x == m and y == n:
ans[0] += 1
return 0
if x < m:
dfs(x+1, y, m, n)
if y < n:
dfs(x, y+1, m, n)
dfs(x, y, m, n)
return ans[0]
Not surprisingly, this method will time out. We need another algorithm to scale down the Time complexity.
b. DP (Dynamic Programming)
DP is Divide-and-Conque (D&C) with Memorization
Take a closer look to is problem, I found that divide-and-conque (D&C) algorithm is really suitable.
The problem f(m, n) could be divided into two parts: f(m, n-1) and f(m-1, n)
Additional, there is only 1 way if m is equal to 1 or n is equal to 1.
So we have the following Recurrence:
f(m,n) = 1, if m = 1 or n = 1
f(m,n) = f(m-1, n) + f(m, n-1)
Implementing the algorithm with python3.
python
def uniquePaths(m: int, n: int) -> int:
dp = [[1]*n] + [[1]+[0]*(n-1) for _ in range(m-1)] # init lookup table
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[m-1][n-1]